
A bitcoin wallet contains one or more pairs of keys, each pair consisting of a private key and a public key. A private key is a randomly generated binary number of 256 bits (a ‘bit’ is either 0 or 1). The person controlling the private keys has access to the associated bitcoins. It is therefore of the utmost importance to keep your private keys secret at all times. The public key is mathematically calculated from the private key, using elliptic curve multiplication. This begs the question: “Is it possible to calculate a private key from a public key?”
It is infeasible to calculate a private key from a public key. The reason being that a public key is calculated from the private key using elliptic curve multiplication, which is a mathematical formula that can only be calculated in one direction.
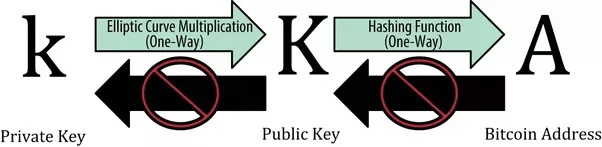
To understand why it is practically impossible to calculate a private key from a public key, let’s start by briefly exploring what we mean by elliptic curve multiplication and why this type of multiplication is irreversible (one-way). Secondly, we will explore the practical implications of this for the security of bitcoin.
What is elliptic curve multiplication?
In mathematics, an elliptic curve is a plane algebraic curve defined by an equation of the form y2 = f(x). Graphically, the elliptical curve can be represented as follows:
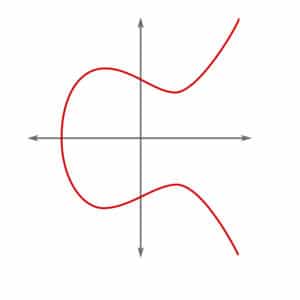
Elliptic curve multiplication is the multiplication of points on an elliptic curve. It is regularly used in cryptography in order to produce one-way mathematical functions.
In computer science one-way mathematical functions are mathematical functions for which it is easy to compute their output when given a certain input, but for which it is practically impossible to compute their inverse functions. In other words, having data ‘x’ it is easy to calculate f(x) but, on the other hand, knowing the value of f(x) it is practically impossible to calculate the value of ‘x’.
How is elliptic curve cryptography used by bitcoin?
Elliptic curve cryptography is the type of public-key cryptography that is used by bitcoin for generating public keys. More in particular, it is embedded in the following formula which is used by bitcoin for generating public keys:
K = k*G
where ‘K’ is the public key, ‘k’ is the private key and ‘G’ called the generator point
The generator point is a predetermined constant point (x,y coordinates) on a specific elliptic curve that is used by bitcoin, as defined in a standard called ‘secp256k1’ (see Figure 2: Illustration of a secp256k1 elliptic curve over the real numbers). This generator point is always the same for all bitcoin users.

By multiplying the private key (k) by the constant generator point (G), another point somewhere on the elliptic curve is generated, which is the corresponding public key (K). No matter which number corresponds to your private key, the corresponding public key will always match another point somewhere on the elliptic curve used by bitcoin.
Now let’s take a closer look at why exactly the public key generated from your private key will always correspond to a point on the elliptic curve used by bitcoin. This will help you better understand why the formula used by bitcoin to generate public keys (i.e. K = k*G, supra) is considered an irreversible one-way function (i.e. it can only be calculated in one direction), making bitcoin cryptographically secure.
Why does a public key generated from a private key always correspond to a point on the elliptic curve?
According to the formula which is used by bitcoin to generate public keys, we need to multiply the private key k by the constant generator point G. Mathematically speaking, this is the same as adding G to itself, k times in a row. Indeed, the most straightforward way of computing a point multiplication is through repeated addition of that point.
If, for illustration purposes, the private key k = 4 this would mean that the public key K = 4*G, which is the same as saying that K = G + G + G + G. Any multiplication of G can therefore be represented by an equivalent addition formula. In other words, your public key is equal to G added by itself as many times as the number of your private key (which is a binary number of 256 bits).
One of the properties of an elliptic curve is that when adding a point on the curve to itself (for example, adding the point G to itself), this is the equivalent of drawing a tangent line (i.e. a straight line that “just touches” the curve at a certain point on the curve) (see Figure 3, Blue lines) at that point, and then reflecting the point where the tangent line intersects the elliptic curve again on the x-axis (see Figure 3, Green lines). Hence, any multiplication of G, will result in another point (x,y coordinates) somewhere on the elliptic curve.
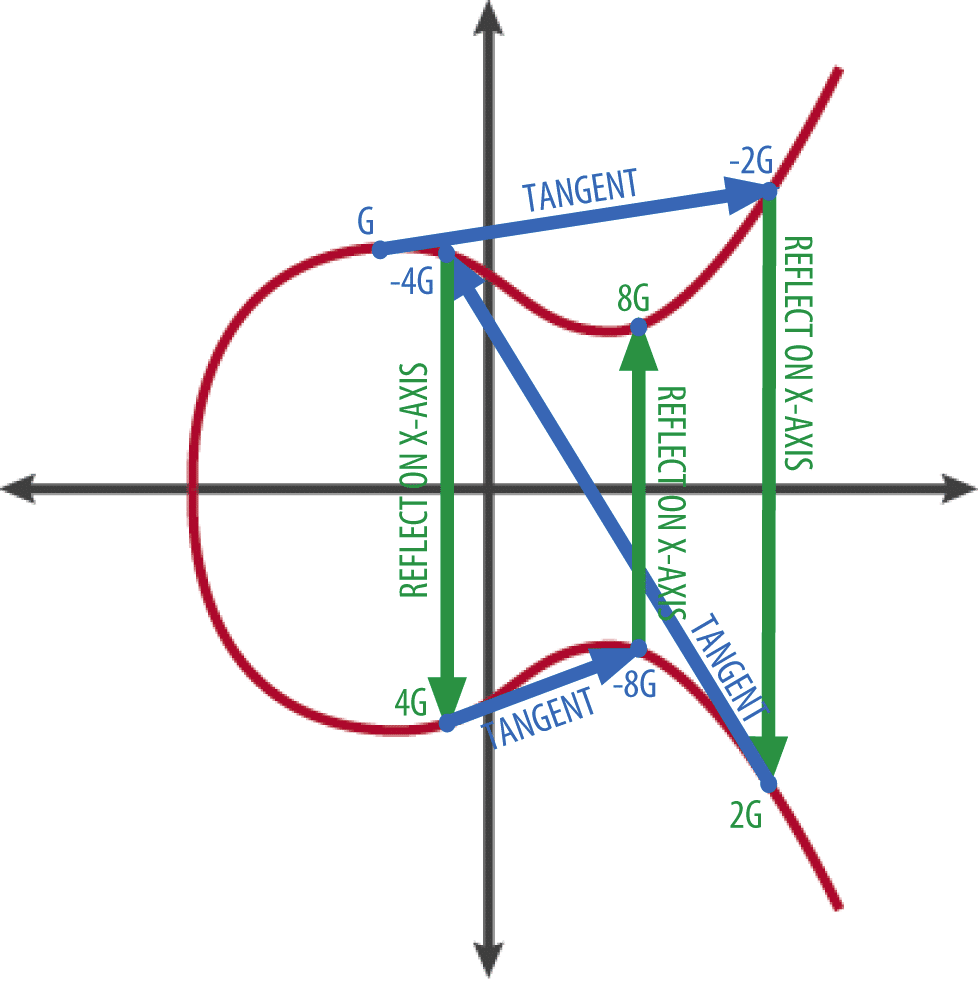
Metaphorically speaking you could think of the calculation of a public key as a hockey puck bouncing around on an ice-skate ring as many times as your private key.
The result is that for a third party (e.g. a hacker) there is no way of knowing how you got to a certain point on the elliptic curve, i.e. how you arrived at your public key. Indeed, the location of a point on the elliptic curve (i.e. the public key) has no immediately obvious relationship to the location of G on the elliptic curve (i.e. the starting point). This is especially true when working with large numbers, such as in the case of bitcoin which uses private keys that are 256 bits long.
To help you better understand this, you could also think about the following similar analogy: say that you have a point Z on a circle. If you would add an angle of 180° to the point Z, you will arrive at a new point on the circle. But if you would add 101 times an angle of 180° to the point Z, you will still end up at the exact same new point on the circle. For an outsider there would therefore be no way of knowing how to reverse the process (i.e. to know how many times an angle of 180° was added to Z to arrive at the end point), except for trying out all the different possibilities one by one.
We have established above that it is impossible for an outsider (e.g. a hacker) to calculate the private key on the basis of a public key, other than by trying out all possible private key combinations in the hopes of generating the corresponding public key by chance. Let us now explore the question whether or not such ‘brute-force’ search method constitutes a realistic threat to the security of bitcoin.
Could someone brute-force search your private key?
We already established that the only way for someone to calculate your private key, is by trying every possible value for your private key and see if it generates the corresponding public key (i.e. by multiplying every possible value of k by G). This is however merely a theoretical possibility which at the present is practically impossible.
As mentioned at the beginning of this article, a private key is simply a binary number of 256 bits that is randomly generated. As such, you could generate your own private key by tossing a coin 256 times in a row and by writing down after each toss either 1 or 0, depending on whether it was heads or tails.
In terms of mathematics, this effectively means that a randomly generated private key could be any number between 1 and 2256 (rounded). In decimal terms, this is equivalent to 1077 possible combinations. In other words, the number of possible private key combinations is inconceivably large. In comparison, the total number of atoms in the observable universe is estimated to be 1080.
The following example will give you an even better sense of how big the number 1077 is. If you would somehow have the ability to generate a billion private keys a second, it would still take you on average 1065 seconds to find a private key that matches someone else’s private key. In fact, even at this rate, the amount of time someone would need to figure out someone else’s private key exceeds the time the universe has existed, based on our common scientific understanding of the age of the universe (i.e. around 13.4 billion years old). Now that is quite a long time if you ask me :-).
Conclusion
The elliptic curve multiplication imbedded in the formula used by bitcoin to generate public keys makes it practically impossible to calculate the corresponding private key.
In addition, the brute-force search method, which could theoretically be used to figure out someone’s private key by trying out all different private key combinations, is from a practical point of view unfeasible. Even with an enormous amount of computing power at your disposal, it would just take too long and consume too much energy.
As long as you store your private keys in a secure environment (i.e. offline, such as on a hardware wallet, as opposed to on an online exchange) your bitcoins are safe.
In this regard we would recommend using a Trezor hardware wallet for storing your bitcoins and other cryptocurrency.
Did you enjoy our article? Feel free to show us your support via the below donation button, allowing us to continue to deliver top quality content:
Attention! Do you store your cryptocurrencies on an online platform? Please note, in that case you are not the actual owner of your cryptocurrencies!
In particular, you run the risk of losing all your cryptocurrencies, without any recourse, in the event that the online platform or your personal account falls victim to hacking or in the event of an unexpected closure (e.g. insolvency) of the online platform.
Protect yourself against hacking and take real ownership of your cryptocurrencies by storing your cryptocurrencies offline on your very own Trezor hardware wallet. Don’t wait before it’s too late and take immediate action now!
Click on the ‘Buy Now’ button below to buy a Trezor wallet from the official Trezor website.


